ジャズと数学
Jazz and Mathmatics

楽譜用紙と白銀比・黄金比

市販の楽譜用紙16段（幅460�o　高さ313�o）

A4版（210×297）

昔は譜面は手書きに決まっていた。楽器屋に行って譜面の用紙を買ってきた。見開き２ページの用紙が使いやすかった。ここにお見せしている”Music Mistro Please”のアレンジはミルス・ブラザースを参考にして1992年に書いた譜面である。

私はComputer人間だから、オタマジャクシの画像をあらかじめ何種類も作っておいて、譜面を書いた時代がある。まだ、MS-DOSのころである。90年代になって譜面作成ソフトを探しに行った。渋谷のヤマハに行ったら、ドイツ製の譜面ソフトが確か20,000円位で売っていた。Notator Logicとかいう物だった。興味半分で使ってみたが、使い勝手の良いものではなかったらしい。すぐに手書きに戻ってしまっている。

その後、2000年代になって使い出したのがFinale 2001Jだった。若くして亡くなったベースの牧島が「先生、これがご推薦です」と教えてくれたものである。これは14年経っても使っている。しかし、Windows XPまでは相性が良かったのだが、Windows 7以降では、仕様の相性が合わないところがある。それで、Finale 2012、Finale 2014を購入して試してみた。どんな種類のソフトも古いVersionほどシンプルで使いやすいのだ。

◆　◆　◆

白銀比（大和比）
　

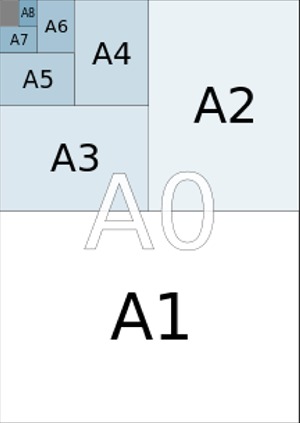
われわれが普段、印刷用に使う紙はA版（A4、A3など）とかB版（B5、B4など）が通常だ。我が家のシャープ複合プリンタでは用紙の引き出しが４段ついているので上記の４種類のサイズが入れてある。普通の家ではA3なんて使わないが、うちは譜面を印刷しなければならない。見開きのA3を使う。

A版はドイツで作られた国際規格ISOの寸法で、原紙A0版は841×1189�oで面積は１ｍ^２、２つ折りして切るとA1版、さらに半分にするとA2版、同様にA3、A4、A5、A6、・・・となる。

我々が使うB版は日本の規格でJISで定められている。B０版は1030×1456�oで１．５ｍ^２である。江戸幕府の公用紙に使われた美濃紙の寸法である。

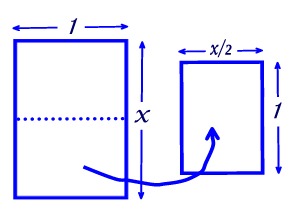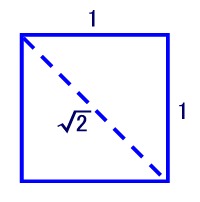
幅＝１、高さ＝Xの紙を半分に切ると、幅＝X/2、高さ＝１になります。

縦横の比が変わらないということは、

１：X＝X/2：１　つまり　X²/2＝1　から　X²＝２

したがって、X＝√２＝１．４１４２１３５６…

これで、１：√２という縦横比の紙を作ると、半分に切っても同じ縦横比が保存されます。

B版の紙は江戸時代の美濃紙の寸法だと言いました。それが、１：√２の縦横比の紙なのです。大きい原紙から小さいサイズの紙にするときに無駄が出ないのです。江戸時代に平方根２が使われていたのです。すごいと思いませんか？

１：√２という比を「白銀比（大和比）」と呼びます。紙のサイズは変わっても相似形なのです。

ところが、冒頭の五線紙は白銀比ではありません。郵便はがき（100×148�o）だって白銀比ではありません。用紙はそのサイズのまま使うもので、半分に切ることを考えていないからです。

ルート２はどうやって測ったのかって？ 対角線を使ったのです。平成人より人間らしいと思いません？ あなたは墓石の対角線の長さの測り方ご存知ですか？江戸時代の人は賢かったのです。簡単に曲尺で測ってしまいます。

長さ＝１の線分を

１：ａ＝ａ：１−ａ　となるようにａ点で分割したい。

ａ²＝１−ａ より　 ａ²＋ａ−１＝0　を解いて、

ａ＝（−１＋√５）/２＝０．６１８０３…

このような線分の分割を「黄金分割」と呼び、０．６１８・・を黄金数と呼ぶ。

関数の最大値（最小値）を与える変数の値を求める問題があります。このような問題は、最適化の問題を数学的に解こうとするときに出てくる問題です。解析的な方法から数値計算の方法まで、いろいろな計算法とその理論があります。実は、このような分野が私の専門分野でした。Operations Reserachの問題にはこのような最適化の問題がたくさん出てきます。

最適化の数値計算の方法に「黄金分割法」という計算法があります。この算法の中で使うキーになる数値が黄金数＝０．６１８なので、中国では「０．６１８法」と呼んでいました。
　

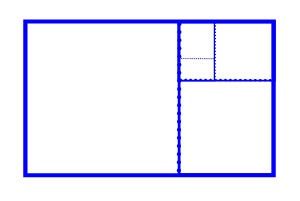縦＝１、横＝１．６１８・・の長方形から１×１の正方形を切り取った残りの長方形の縦横比は１：１．６１８・・になる。黄金長方形と呼ばれる。

１：１．６１８…を黄金比と呼ぶ。

ギリシャ建築に黄金比が使われたとか、バランスが美しく見えるのは、黄金比を用いているからだとか、そういうこじ付け話が美術やデザインの本にごろごろ出てきます。

１９世紀の終わりごろからマンハッタンのど真ん中に音楽出版社が集まってきました。当時はレコードはまだ普及していません。音楽を売ること＝譜面を売ることだったのです。この地域はTin Pan Alleyと呼ばれ、１９５０年代初めまで続きました。

⇒　Tin Pan Alley

左の楽譜はSheet Musicと呼ばれ、ピアノの伴奏がついています。また、半端な寸法の用紙に印刷されています。1940年に出版されたオリジナルの楽譜です。