新型コロナウィルス感染について

古林　隆

（2020/5/1）

昨年（2019年）12月に中国武漢で発生したと思われる新型コロナウィルス（COVID-19）が，今年2月以降世界中で猛烈に流行している．日本では，以前から手洗い，うがい，マスク着用の習慣が，他国より浸透しているから，感染拡大のスピードが遅いように思えるが，それでも，感染者数が3,000人を超えた4月7日緊急事態宣言が出された．

4月27日現在，感染者数は，全国で13,600人，東京都で3,900人に達し，死者は，全国394人，東京都100人である．ただ，ここでの「感染者」は，PCR検査を受けて陽性であった人のことである．当然のことながら，PCR検査を受ける人が増えれば，「感染者」も増えることになる．「感染者数」や「感染率」のようにいろいろな数値が報道されるが，その中には，滑稽な表現や誤解して（意味を取り違えて）報道されるものがある．いくつか取り上げてみた．

１． 感染者数
日本では，1月末に武漢から帰国した人が感染者第1号である．それ以来，毎日感染者数，正確に言えば累積感染者数が報道されている．最近は，日別感染者数の方が重要視されているようであるが，2月中には，感染者数のグラフを示して，「増えていますね」というアナウンサーがいて，笑ってしまった．累積が減少したらおかしいだろ!!!

累積感染者数を示すときは，「累積感染終了者（陽性から陰性になった人）数」（4月27日で2,900人）も示すべきである．その差が小さくなることが，「感染が収まる」を意味するであろう．

２． 日別感染者数
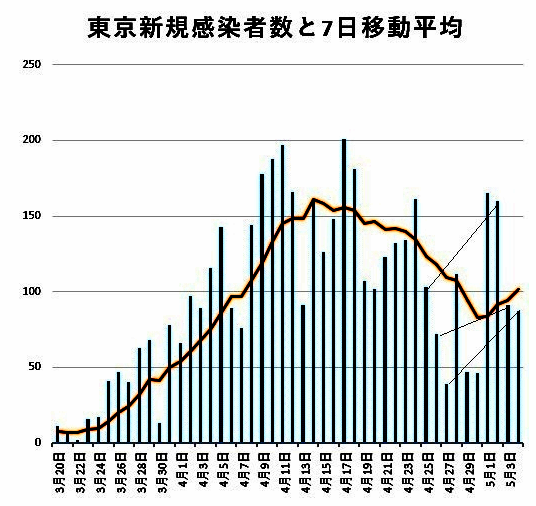
最近は，1日ごとに新たに判明した感染者の数が注目されるようになった．棒グラフで示すのは，適切だが，この感染者数は，検査数によるから，日曜月曜の発表人数は，他の曜日に比べて，明らかに少ない．7日間の周期性があるのがわかっているのだから，最近7日間の平均感染者数のグラフを示せばよい．「他の局とちがう表し方をしよう」と考える気の利いたディレクターがいないのに失望する．（*1）

緊急事態宣言が出て以来，外出自粛の効果を示すために，日別感染者の予測数を近似するグラフが表示されるようになった．基準日からの日数xと日別感染者数ｙの関係は，指数関数ｙ＝A・B^x で表わされている．このグラフの形状は，Bと1との大小関係で増減を変えるが，いずれも下に凸である．詳しいことはわからないが，Bは，一人の一日当り接触者数の平均Ｃに比例するようである．「接触者」の定義は不明であるが，外出者一人の一日当り接触者数の平均を一日の外出者数Ｇに関係なく一定とし，外出しない人の接触者数を無視すると，Ｃは，Ｇに比例する，したがって，Bも，Ｇに比例する，（*2）Ｇが平常時の6割減（4/10）になった時に，B＝1になるそうで，それより小さくなれば，日別感染者数は，“急激に”減少する．ただ，示されたグラフでは，基準日以前（外出自粛前）のB＞１である曲線と基準日以降のB＜1の曲線をつないでいるので，刃物の先のように尖がっていて，不自然であり，安心感（信頼感）を持てない．不確定要素が多い状況での予測値であるから，（平均化して）滑らかにしてほしいものである．

（*1）28日のテレビ番組に出演していたJ大学H教授は，「7日分をまとめて見るべきだ．」と発言していた．
（*2）外出者一人当たりの接触者数の平均がＧによることも考えられる（この平均がＧに比例すれば，BはＧの2乗に比例する）が，かなり複雑になるので，ここでは，採用されていないと思われる．

３． 陽性率と感染率
4月に入って，陽性率と感染率という言葉がよく出るようになったが，二つを混同している場合が多いし，標本と母集団の区別ができていないのに大きなことを言う「やから」がいてうんざりする．

検査を受けた人N人の内M人が陽性であったから，「陽性率は，M /Nである．」というのは，検査を受けた人の陽性率という意味で正しいが，この値が，感染率として使われることがある．感染率が重要であることは，京都大学の山中教授が言うように当然であるが，「ある集団の中での感染者の割合」という意味の感染率は，その集団すべてを検査できない場合，推測せざるを得ない．報道された陽性率と推測したい感染率との関係がほとんどないのに，感染率という言葉を使うのが気になる．先日，K病院外来患者の陽性率が約6％であると発表されたとき，ニュース解説番組のレギュラー出演者の一人が，「ジョギングしている人の中にも，6%の感染者がいるから，・・・」と発言したので，抱腹した．病院に来る人達の感染率とジョギングできる人達のそれが同じだと思っているのか!!!　標本から得られた数値は，母数（母集団の特性値）の推定値（推測する値）になりうるが，それには，その標本が母集団から無作為に取られたというのが　大前提である．標本が小さい（測定されたものの数が少ない）と推測の精度が悪くなるので，検査数が少なすぎることを指摘する人は，ときどきいるが．無作為でない（偏りがある）標本はいくら大きくても役に立たない．（上記の陽性率は，感染率の上限としては使えるであろう．）テレビで大きな口をたたく人なら，これくらいの推測統計の知識を持っていてほしいものである．

新型コロナウィルス感染について（追記　2020/5/3）

テレビ局が，スタジオの公開番組やロケを自粛して，番組の作成に苦慮しているのは重々わかっているが，昨日（5月2日）もひっかかる紹介番組があった．いちごのケーキで人気のあるケーキ屋を紹介していた．若い女性客の長蛇の列の映像に続いて，おいしそうに食べているところが映っていた．再放送であることに気づいて，よく見たら「今は休業しています」と字幕が出ていた．今放映する番組じゃないだろ!!!

２． 日別感染者数（続き）
ここで使っている日別感染者数は，報道では「新規感染者数」と言われている．うれしいことにBに立派な名前がついた．「実効再生産数」である（読みから変換するのに，うっかり「さいせい（再生）」で切ったら，「算数」が出てきた）．自分達でデータを取れる製造業や市場調査（選挙を含む）とちがって，押しつけられたデータだけで推測モデルを作成するのは，いろいろ苦労（迷い？）が多いことであろう．モデル作成の関係者から，「きれいごとを言っていたら，何もできない」と言われそうだ．ただ，押しつけられるデータの中には使える部分とそうでない部分があるから，前者を取り上げれば，もう少し細かなモデルが出来るのではないかと思う．新規感染者数では，感染経路不明の感染者数と病院内感染のようなクラスター内の感染者数は，別に考えるべきである．外出自粛の対象になる超大集団のモデルに，大きさも，その中での実効再生産数も，大きくかけ離れているクラスターのデータを使うのは，どだい無理である．昨日の朝日新聞に掲載されていたグラフでは，感染経路不明の感染者数がわかりやすかった．これにスポットを当てるメディアがあってもよいのにと思う．

後記
今日は，とりあえずここまでです．文章にすると，きつくなっているような気がしますが，「とんちんかんな」報道を取り上げているだけです．

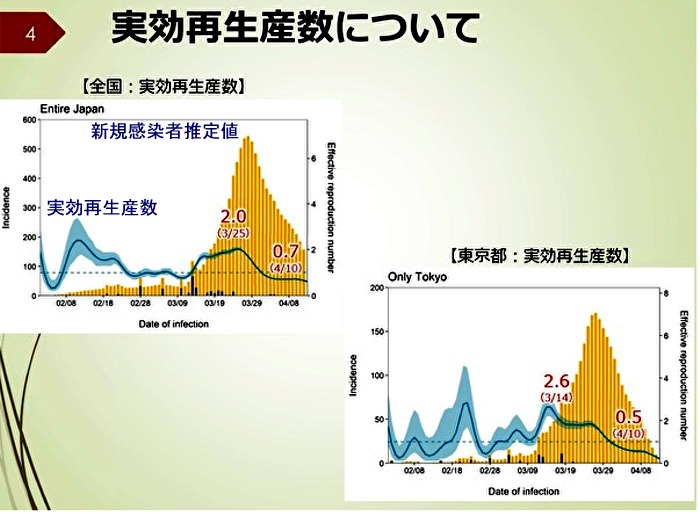
新型コロナウィルス感染について（追記　2020/5/4）

次から次へと気になる報道が出てくるのであきれてしまう．

今日（5月4日）は，増減が激しい実効再生産数のグラフ(*1)を見てびっくり仰天した．まず，昨日の文章を訂正する．Bは，実効再生産数ではなかった．実効再生産数は，単なるデータであった．「一人の感染者が新たに感染させる人の平均数」という説明がついているが，正しくは，「感染させた人の平均数」である．詳しいことは不明だが，その日のクラスター毎の新規感染者数をもとに計算していると思われるから，日毎に増減するのは当然である．（感染経路不明の感染者については，計算の仕様がない．）しかし，外出自粛などの効果を見るために必要なのは，感染させる人の数である．「この値が1より小さければ，感染は収まる・・・」という時の値は，後者のことである．これは，日毎に変わるものではないが，基準日（外出自粛要請開始日）で変化（減少）するから外出自粛の効果が評価できる．データの話とモデルの話がごちゃごちゃになっているのは，専門家の説明がわるいのか報道の仕方がわるいのかわからないが，毎日内容を理解するのに，脳をフル回転させられて，ありがたい．

(*1) 実効再生産数のグラフは，5月2日の朝刊に出ていたのに，見落としていた．

新型コロナウィルス感染について（追記　2020/5/5）

昨日，指数関数モデルの底に使われるBが，日毎に変動するように見えて，「Bは実効再生産数ではなかった」と書いたが，「Bは実効再生産数である」と言っても間違いではなさそうである．

そもそも，データの話とモデルの話をごちゃまぜにして説明しているのが，筋道をわかりにくくしている．実効再生産数は，二つの意味で使われているようだ．「感染させた平均人数」という意味であれば，日毎に変動してもおかしくないのかもしれない（こんな値を日毎に計算してもあまり意味がないから，せめて，一週間単位で計算すればよいのにと思う）．

問題は，これがモデルで使われる「感染させる平均人数」のように説明していることである．「感染させる平均人数は，昨日は2.4であったが，今日は0.8であった」という説明は，さいころを毎日何回かふって1の目が出た回数から，「1の目が出る確率は，昨日は0.17であったが，今日は0.15であった」と言っているようなものだ．「感染させる平均人数」は，ある期間は変わらないと考えるべき（モデルとは，そういうものである）で，その意味の実効再生産数であれば，「Bは，実効再生産数である」と言ってもよい．

今日（5月5日）「ある国（国名を聞き逃した．多分ドイツ）で計算した実効再生産数は，平常時で2.5 であった」というのを聞いて，なぞときができた．2.5ｘ(4/10)＝1 であるから，（6割減）＝（感染者増減なし）というストーリーができあがったのであろう．しかし，どうして日本のモデルの平常時のBの値に他国の値が使われるのであろう．奇々怪々である．この値こそ，緊急事態宣言以前の（クラスター以外の）感染者数に指数関数をあてはめて求めればよいのにと思う．

どのように解釈すれば筋道が通るのかを考えていると，よい脳トレになって，楽しい．

新型コロナウィルス感染について（追記　2020/5/6）

毎朝，「どんなとんちんかんなことが出てくるのだろう」と期待しながら，テレビのニュース関連番組を見ているが，今日は，うれしいことにその期待がはずれて，まさに「これだ」というグラフが出て来た．それは，大阪モデルで表示された「感染経路不明者の7日間移動平均数」である．多少凸凹はあるが，その形に見とれてしまった（大げさ）．大阪府の関係者に拍手を送りたい．解説者のその後の発言が痛快であった．

「トップ（ここでは知事）がよくわかる人であれば，支える人は頑張ります」

新型コロナウィルス感染について（追記　2020/5/10）

検査数
毎日感染者検出のための検査数のことが取り上げているが，「検査数をもっと増やすべきだ.」というのを耳にタコができるほど聞かされてうんざりする．検査関係者の中には，「現場を知らない人に，勝手なことを言ってほしくない」と思って苦虫を噛んでいる人が多いことであろう．

私なりにまとめておく
(1) 医療（治療）の立場からも予測の立場からも検査数は多い方がよい

検査をする対象は両者で異なる．前者では，“あやしい”人を優先して検査すべきであるが，後者では，偏りをなくしたい．初期段階では，前者をとるのは，当然のことである．　

余裕があれば，後者の検査もすればよいが，現状は，そうではないと思われる．

(2) 検査体制（要員，設備）が，他の国（特に韓国）より貧弱である

だから，「検査件数が少ない」という説明にはなるが，今すぐに「検査件数を増やす」こととは結びつかない．来年度予算を決めるときには，厚生労働省に頑張ってもらたいから，その時期に大々的に取り上げてほしいものである．

(3) 現状でも検査数を増やす方策が提案されていて，すでに実行されているものもある

検査に大学の研究者を動員する，大学の研究用の検査機器を使う，より手間のかからない検査方法を採用するなどである．

報道番組としては，ただ「検査数をもっと増やすべきだ」とわめくのではなくて，(3)に挙げたように，「こうすれば増やせます」という内容を取り上げてほしいものである．（非難より提案に力を入れてほしい）

◆

5月8日には，なんとも不思議な報道があった．K大学の元物理学教授が，「検査数を増やせば，感染を早く収束できる．」との趣旨の主張をしたそうである．指数モデルのBの値で言えば，検査数を増やせば，小さくなるということである．具体的には，「検査数を2倍にすれば，外出者数を8割減にするときの効果を，5割減で達成できる．」そうである．「検査数を2倍にして求めたモデルでは，外出者数を5割減にするだけで，感染者数が，元のモデルで外出者数を8割減にするときのそれより少なくなる」の方がわかりやすいかもしれない．

スペイン風邪の流行の時のモデルを基に考えられた難解な筋道は，素人には，マジックの世界であるが，「検査数（標本の大きさ）を変えるだけで，モデル（母集団）の特性値が変わる」のは，直感的に受けいれられない．報道によれば，検査して陽性であった人は，隔離されることになっているそうで，ここにからくりがありそうである．

隔離される人は，市中（外出自粛対象になる人達）から除かれるから，市中の感染率は，検査数が多くなれば，小さくなる．（不良品をいくつか除けば，残りの不良率は下がる．）これくらいの説明でとりあえず納得することにしたが，人口約1,400万人に対して，検査数せいぜい数万，陽性者数は，その数％である東京都で，検査数を2倍にするだけで，こんなに影響がでるのだろうかという疑問は残る．

新型コロナウィルス感染について（追記　2020/5/11）　

うれしいことに，質問をいただきました．

＜質問＞
ランダムサンプリングが出来ると仮定して東京都の人口1400万人に対して何人の人にPCR検査をすれば、まあ信頼できる結果が出せますか．

＜答＞
2,500人検査すればいいでしょう．

ある集団の中の感染者の割合という意味での「感染率」を推定するのに，検査数と集団の大きさの比が1/20以下くらいになれば，集団の大きさは関係ありません． したがって，以下の説明は，どの都道府県でも通用します．
感染率ｐの値が含まれると思われる区間を示すのを区間推定といいます．精度（区間の幅）は，検査数ｎと感染率ｐによります. 区間の中心は，ｐとし，中心から端までの長さ（幅の半分）ｄを定めて，ｐ＋ｄを上側限界値，ｐ−ｄを下側限界値とします．幅の定め方によって，ｎの計算式が変わります．

H1：幅をｐの8/10（ｄ＝4/10×ｐ）にしたいとき
　　ｎ＝25×(1―ｐ)／ｐ 　 （下記の＜参考＞を参照されたい）

H2：幅をｐの1/2（ｄ＝1/4×ｐ）にしたいとき
　　ｎ＝64×(1―ｐ)／ｐ

このように，ｎは，幅の2乗に逆比例します．（幅を1/2にすれば，ｎは，4倍になります．）ｐを1％（報道されている陽性率は，数％ですが，これは，感染してそうな人ばかり検査した結果ですから，市中では，もっと小さいはずです．）とすると，検査数ｎは，H1 では 2,500，H2では 6,300になります．ｐを3％にすれば，それぞれ800，2,100 になります．

ｐの値は未知ですから，幅は，陽性率qを求めた後，次のように計算します．

�@ e＝２×（（q×(1−q)／ｎ）の平方根）を計算する．

�A 上側限界値を q＋e とし， 下側を q−e とする．

たとえば，ｎ=2,500で，陽性者数が30であれば，q＝0.012, e＝0.004となるので，

「感染率ｐの推定値は，0.012であり，ｐは，0.008と0.016の間にある」ということになります．

幅をｐの8/10にするのは，かなり荒っぽい気もしますが，感染率のように，値が小さい（１％前後である）場合，1日の検査数は少なくして，日を改めて検査した方が，役に立つデータが得られると思います．

＜参考＞
さいころを何回かふるとき，1の目が出る回数のように，同じ行為を一定回数繰返すときに，注目している現象が出現する回数の分布を二項分布と言います．繰返し回数をｎ，出現率をｐとする二項分布では，出現比率（出現回数とｎの比）の標準偏差は，（（ｐ×(1−ｐ)／ｎ）の平方根）です．推定区間の幅を標準偏差の4倍，ｄを標準偏差の2倍にするのが一般的ですから，H1のｎの計算式は，

２ｘ（（ｐ×(1−ｐ)／ｎ）の平方根）＝ 4/10×ｐ

より，導かれます．

ある集団の中から（無作為に）標本をとって，注目している特性を持つものの個数を数えるとき，標本の大きさと集団の大きさの比率が，十分小さければ，その個数の分布は，二項分布で近似してよいことになっています．